Coning (countersteering*): The Physics Of Motor Scooter Dynamics For Dummies (abridged)
If you prefer simple go to the video link** at the bottom, or read on and be baffled...
www.wikipedia.org
A single-track vehicle such as a motor scooter is an inverted pendulum —it will fall over unless balanced.
External forces on a bike and rider leaning in a turn: gravity in green, drag in blue, vertical ground reaction in red, net propulsive and rolling resistance in yellow, friction in response to turn in orange, and net torques on front wheel in magenta.
Lateral dynamics has proven to be complicated, requiring three-dimensional, multibody dynamic analysis with at least two generalized coordinates to analyze. At a minimum, two coupled, second-order differential equations are required to capture the principal motions. Exact solutions are not possible, and numerical methods must be used instead. Competing theories of how bikes balance can still be found in print and online. On the other hand, as shown in later sections, much longitudinal dynamic analysis can be accomplished simply with planar kinetics and just one coordinate.
Lateral Force Generation as Slip Angle Grows
The history of the study of bike dynamics is nearly as old as the bicycle itself. It includes contributions from famous scientists such as Rankine, Appel and Whipple. In the early 1800s Karl von Drais, credited with inventing the two-wheeled vehicle variously called the laufmaschine, velpcipede, draisine, and dandy horse, showed that a rider could balance his device by steering the front wheel. By the end of the 1800s, Emmanuel Carvallo and Francis Whipple showed with rigid-body dynamics that some safety bicycles could actually balance themselves if moving at the right speed. It is not clear to whom should go the credit for tilting the steering axis from the vertical which helps make this possible.
In 1970, David Jones published an article in Physics Today showing that gyroscopic effects are not necessary to balance a bicycle. Since 1971, when he named the weave and capsize modes, Robin Sharp has written about the mathematical behavior of motorcycles and bicycles, and his work has continued to the present day with David Limebeer. Both men were at Imperial College, London. In 2007, Meijaard, Papadopoulos, Ruina, and Schwab published the canonical linearized equations of motion, in the Proceedings of the Royal Society A , along with verification by two different methods
The Draisine
Trail is a function of head angle, fork offset or rake, and wheel size. Their relationship can be described by this formula:
where Rw is wheel radius, Ah is the head angle measured clock-wise from the horizontal and Of is the fork offset or rake. Trail can be increased by increasing the wheel size, decreasing or slackening the head angle, or decreasing the fork rake.
The more trail a bike has, the more stable it feels.
Gyroscopic effect on front wheel of a bike. Appling a torque (in green) about the lean
axis results in a reaction torque (in blue) about the steer axis.
The role of the gyroscopic effect in most bike designs is to help steer the front wheel into the direction of a lean. This phenomenon is called precession and the rate at which an object precesses is inversely proportional to its rate of spin. The slower a front wheel spins, the faster it will precess when the bike leans, and vice-versa. The rear wheel is prevented from precessing as the front wheel does by friction of the tires on the ground, and so continues to lean as though it were not spinning at all. Hence gyroscopic forces do not provide any resistance to tipping.
At low forward speeds, the precession of the front wheel is too quick, contributing to an uncontrolled bike’s tendency to oversteer, start to lean the other way and eventually oscillate and fall over. At high forward speeds, the precession is usually too slow, contributing to an uncontrolled bike’s tendency to understeer and eventually fall over without ever having reached the upright position. This instability is very slow, on the order of seconds, and is easy for most riders to counteract. Thus a fast bike may feel stable even though it is actually not self-stable and would fall over if it were uncontrolled. A bicycle wheel with an internal flywheel for enhanced gyroscopic effect is under development as a commercial product, the Gyrobike, for making it easier to learn to ride bicycles.
Graphs showing the lean and steer angle response of an otherwise uncontrolled bike, traveling at a forward speed in its stable rangle (6 m/s), to a steer torque that begins as an impulse and then remains constant. Torque to right causes initial steer to right, lean to left, and eventually a steady-state turn to left.
Countersteering is required to turn any tandem 2-wheeled vehicle
A hypothetical curve on dry asphalt
Another contribution of gyroscopic effects is a roll moment generated by the front wheel during countersteering. For example, steering left causes a moment to the right. The moment is small compared to the moment generated by the out-tracking front wheel, but begins as soon as the rider applies torque to the handlebars and so can be helpful in motor scooter racing. For more detail, see countersteering below.
This is how countersteering works
When riding no-hands. To turn left, a rider applies a momentary torque, either at the seat via the legs or in the torso that causes the bike itself to lean to the right, called counter lean by some authors. The combined center of mass of the bike and rider is only lowered, of course. However, if the front of the bike is free to swivel about its steering axis, the lean to the right will cause it to steer to the right by some combination of gyroscopic precession (as mentioned above), ground reaction forces, gravitational force on an off-axis center of mass, or simply the inertia of an off-axis center of mass, depending on the exact geometry and mass distribution of the particular bike, and the amount of torque and the speed at which it is applied.
1968 Vespa VLB Vintage Scooter 150cc Sprint currently (07/20/2010) for sale on ebay, Current bid: US $2,136.00. Time left:2d 21h (Jul 23, 201010:40:30 PDT). Reserve not yet met.
http://tinyurl.com/2dqff65 This countersteering to the right causes the ground contact to move to the right of the center of mass, as the bike moves forward, thus generating a leftward lean. Finally the front end steers to the left and the bike enters the left turn. The amount of leftward steering necessary to balance the leftward lean appropriate for the forward speed and radius of the turn is controlled by the torque generated by the rider, again either at the seat or in the torso.
To straighten back out of the turn, the rider simply reverses the procedure for entering it: cause the bike to lean farther to the left; this causes it to steer farther to the left, which moves the wheel contact patches farther to the left, eventually reducing the leftward lean and exiting the turn.
The reason this no-hands steering is less effective on heavy bikes, such as motorcycles, is that the rider weighs so much less than the bike that leaning the torso with respect to the bike does not cause the bike to lean far enough to generate anything but the shallowest turns. No-hands riders may be able to keep a heavy bike centered in a lane and negotiate shallow highway turns, but not much else.
*ALL THAT BABBLE SAID, JUST CLICK THIS LINK TO THIS SIMPLE VIDEO
countersteering 101
*Steering a (motor scooter) is counterintuitive; to turn right, you must steer left initially, and vice versa. You can execute this initially counter-directed turn by turning the handlebars explicitly (called counter-steering) or by throwing your hips to the side. Contrary to common belief, gyroscopic forces play only a limited role in balancing and steering. [D. E. H. Jones, Phys. Today 23 (4), 34–40 (1970)]. ©2000 American Association of Physics Teachers.
Posts
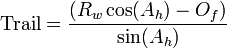
"I don't see it???"
ReplyDelete